TAREA 3. INTENSIVOS Y EXTENSIVOS

Propiedades intensivas:

Son aquellas que quedan totalmente determinadas dando un sólo número real y una unidad de medida, es decir no dependen de la orientación. Ejemplos de este tipo de magnitud son la longitud de un hilo, la masa de un cuerpo o el tiempo transcurrido entre dos sucesos. Se las puede representar mediante segmentos tomados sobre una recta a partir de un origen y de longitud igual al número real que indica su medida. Otros ejemplos de magnitudes escalares son la densidad; el volumen; el trabajo mecánico; la potencia; la temperatura.

Propiedades extensivas:

El desplazamiento, la velocidad, la aceleración, la fuerza, el campo eléctrico, etc., que no quedan completamente definidas dando un dato numérico, sino que llevan asociadas una dirección. Estas últimas magnitudes son llamadas extensivas o  vectoriales en contraposición a las primeras llamadas escalares.

Las magnitudes vectoriales quedan representadas por un ente matemático que recibe el nombre de vector. En un espacio euclidiano, de no más de tres dimensiones, un vector se representa por un segmento orientado. Así, un vector queda caracterizado por los siguientes elementos: su longitud o módulo, siempre positivo por definición, y su dirección, la cual puede ser representada mediante la suma de sus componentes vectoriales ortogonales, paralelas a los ejes de coordenadas; o mediante coordenadas polares, que determinan el ángulo que forma el vector con los ejes positivos de coordenadas.

Se representa como un segmento orientado, con una dirección, dibujado de forma similar a una "flecha". Su longitud representa el módulo del vector, la recta indica la dirección, y la "punta de flecha" indica su sentido.

Magnitudes Intensivas	Magnitudes Extensivas
Longitud	Velocidad
Densidad	Fuerza
Volumen	Aceleración
Potencia	Movimiento
Temperatura	Momento Angular
Trabajo mecánico	Superficie
Campo magnético	Inducción magnética
Campo eléctrico	Inducción eléctrica.

Tarea 2. SPIN

2A.
Un electrón ligado a un átomo gira sobre sí mismo, pero no podemos calcular su momento angular de rotación del mismo modo que calculamos el de la Tierra.
La idea de que el electrón tiene un movimiento de rotación fue propuesta en 1926 por G. Uhlenbeck y S. Goudsmit para explicar las características de los espectros de átomos con un solo electrón. La existencia del espín (rotación) del electrón está confirmada por muchos resultados experimentales, y se manifiesta de forma muy directa en el experimento de Stern-Gerlach, realizado en 1924.
En la simulación de este experimento, se comprobará la existencia del espín del electrón observando que un haz de átomos se divide en dos trazas simétricas al eje X. A partir de la medida de la desviación del haz, determinaremos el valor del magnetón de Bohr.
La simulación es similar al experimento de Thomson que realizamos para determinar la naturaleza de los denominados rayos catódicos y medir la razón entre la carga y la masa del electrón.

Se postula la existencia de un momento angular intrínseco del electrón llamado espín S. Como el electrón es una partícula cargada, el espín del electrón debe dar lugar a un momento magnético µ, intrínseco o de espín. La relación que existente entre el vector momento magnético y el espín es

Donde g se denomina razón giromagnética del electrón, su valor experimental es aproximadamente 2.

El número de orientaciones del vector momento angular respecto a un eje Z fijo es 2S+1, tenemos para el caso del espín S=1/2 que la componente Z tiene dos valores permitidos  . Por lo que mB se denomina magnetón de Bohr.

Sabiendo que carga del electrón e=1.6·10^-19 C, la masa m=9.1·10^-31 kg y la constante de Planck h=6.63·10^-34/(2p) Js. Obtenemos m_B =9.27 10^-24 Am².

La energía de un dipolo magnético  µ en un campo magnético B que tiene la dirección del eje Z es el producto escalar

U=-µ·B=-µ_z·B=±µ_B·B

Si B es variable en la dirección Z, el dipolo magnético experimenta una fuerza

que lo desviará de su trayectoria rectilínea. Si el dipolo magnético es paralelo al campo magnético, tiende a moverse en la dirección en la que el campo magnético aumenta, mientras que si el dipolo magnético es antiparalelo al campo magnético se moverá en la dirección en la que el campo magnético disminuye.

En el experimento se usa un haz de átomos hidrogenoides, como plata, litio, sodio, potasio y otros que constan de capas electrónicas completas salvo la última en la que tienen un electrón. El momento angular orbital l de dicho electrón es cero, por lo que está en el estado s.

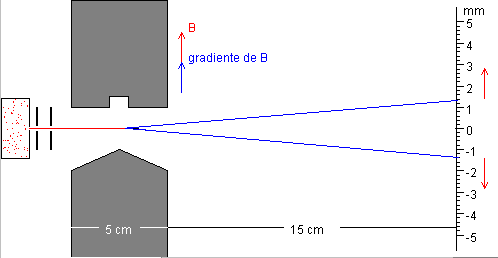
Se selecciona un haz de átomos de una velocidad dada y se le hace atravesar una región en la que existe un campo magnético no homogéneo, tal como se muestra en la figura.

1.     Movimiento del átomo en la región en la que se ha establecido un gradiente de campo magnético
Suponiendo que el gradiente de campo magnético es constante, la aceleración a lo largo del eje Z es constante, a lo largo del eje X es cero. Tenemos un movimiento curvilíneo bajo aceleración constante.

Si la región en la que hay un gradiente de campo magnético tiene una anchura L, la desviación que experimenta el haz, véase la figura, vale

1.     Movimiento del átomo fuera de dicha región
Cuando el átomo de masa m abandona la región en la que hay un gradiente de campo magnético, sigue una trayectoria rectilínea con velocidad igual a la que tenía al abandonar la citada región. Las componentes de la velocidad serán

La desviación total en la pantalla será

Midiendo d despejamos en dicha ecuación el valor m_B del magnetón de Bohr.
 

2B. Experimento de Stern-Gerlach

Se calienta una sustancia paramagnética en un horno que emite un haz de átomos hidrogenoides eléctricamente neutros con la misma velocidad v, que siguen una trayectoria rectilínea hasta que se encuentran en una región en la que hay un gradiente de campo magnético. Sobre la placa de observación colocada perpendicularmente al haz observamos dos trazas finas del haz. Estas trazas son simétricas respecto de la dirección incidente, tal como se ve en la figura.
Los resultados del experimento indican que el hecho de que se obtenga dos trazas distintas y simétricas prueba que el momento magnético no puede tomar más que dos orientaciones con respecto al campo magnético B. El momento magnético m del átomo es igual en módulo al magnetón de Bohr m_B.

La simulación que se describe en esta página complementa la experiencia de Stern-Gerlach y comprueba que el momento magnético medio de los átomos depositados en la placa es inversamente proporcional a la temperatura absoluta (ley de Curie).

La energía de un átomo de momento magnético m en el campo magnético B viene dado por el producto escalar

E=-m·B

• Para los átomos cuyo momento m  es paralelo a B vale  E₁=-μ_BB
• Para los átomos cuyo momento m es antiparalelo a B vale E₂=+μ_BB

Los átomos pueden estar en uno u otro de los dos niveles de energía E₁ y E₂. Aplicando la fórmula de la distribución de Boltzmann podemos calcular la proporción de átomos que ocupan cada uno de los dos niveles de energía

Naturalmente, n₂=1-n₁

n₁ es mayor que n₂, ya que la exponencial decreciente en el denominador no puede ser mayor que la unidad, ni menor que cero. Por tanto, hay más átomos con el momento paralelo al campo magnético que con el momento magnético apuntando en sentido contrario al campo. La sustancia presenta un momento magnético no nulo.

<m>=n₁ m_B+n₂(-m_B)

Como es mucho menor que la unidad (por ejemplo, si B=1 T y la temperatura T=300 K el cociente vale 0.0045. Téngase en cuenta que m_B=9.3 10^-24 A m², y k=1.38 10^-23 J/K), utilizando el desarrollo en serie e^x=1+x+... se obtiene

El momento magnético medio es inversamente proporcional a la temperatura absoluta de la sustancia, el comportamiento de los materiales paramagnéticos.

2C. Tabla de partículas

Leptones

	Leptones cargados				Neutrinos
	Nombre	Símbolo	Carga	Masa en reposo (MeV)	Nombre	Símbolo	Carga	Masa en reposo (MeV)
1ª generación	Electrón		−1	0,511	Neutrino electrónico		0	< 3·10−6
	Positrón		+1		Antineutrino electrónico		0
2ª generación	Muon		−1	105,658	Neutrino muónico		0	< 0,19
	Antimuón		+1		Antineutrino muónico		0
3ª generación	Tauón		−1	1776,99	Neutrino tauónico		0	< 18,2
	Antitauón		+1		Antineutrino tauónico		0

Bosones

Nombre	Símbolo	Carga eléctrica (e)	Carga de color	Espín	Masa en reposo (GeV/c²)	Existencia	Vida media	Desintegraciones más importantes
Fotón		Neutra	Neutra	1	Nula	Confirmada	Estable	---
Bosón W		± 1	Neutra	1	80,425	Confirmada	3·10-25
Bosón Z		Neutra	Neutra	1	91,187	Confirmada	3·10-25	---
Gluón	g	Neutra	Color + Anticolor	1	Nula	Confirmada	Estable	---
Gravitón	G	Neutra	Neutra	2	Nula	Hipotética	Estable	---
Bosón de Higgs	H	Neutra	Neutra	0	≈ 125.5	Confirmada	Inestable

Hidrogeno

Cuando se examinan las líneas del espectro del hidrógeno a una resolución muy alta, se encuentran que son dobletes poco espaciados entre sí. Esta división se llama estructura fina y fue una de las primeras evidencias experimentales del espín electrónico.

Las pequeñas divisiones de la línea espectral, se atribuye a una interacción entre el espín del electrón S, y el momento angular orbital L. Se le llamainteracción spin-órbita.

De acuerdo con la teoría de Bohr, la conocida línea roja del hidrógeno, H-alfa, es una sola línea. La aplicación directa de la ecuación de Schrödinger al átomo de hidrógeno, da el mismo resultado. Si se calcula la longitud de onda de esta línea, usando la expresión de energía de la teoría de Bohr, se obtiene 656,11 nm para el hidrógeno, considerando el núcleo como un centro fijo. Si se utiliza la masa reducida, se obtiene 656,47 nm para el hidrógeno y 656,29 nm para el deuterio. La diferencia entre las líneas del hidrógeno y el deuterio, es de aproximadamente 0,2 nm y la división de cada una de ellas es de alrededor de 0,016 nm, correspondiente a una diferencia de energía de alrededor de unos 0,000045 eV. Esto corresponde a un campo magnético interno sobre el electrón, de aproximadamente 0,4 Tesla

Existen dos tipos distintos de moléculas diatómicas de hidrógeno que difieren en la relación entre los espines de sus núcleos:

·         Orto - hidrógeno: los espines de los dos protones se encuentran paralelos y conforman un estado triplete.

·         Para - hidrógeno: los espines de los dos protones se encuentran antiparalelos y conforman un estado singlete.

En condiciones normales de presión y temperatura el hidrógeno gaseoso contiene aproximadamente un 25% de la formapara y un 75% de la forma orto, también conocida como "forma normal". La relación del equilibrio entre orto - hidrógeno y para - hidrógeno depende de la temperatura, pero puesto que la forma orto es un estado excitado, y por tanto posee una energía superior, es inestable y no puede ser purificada. A temperaturas muy bajas, el estado de equilibrio está compuesto casi exclusivamente por la forma para. Las propiedades físicas del para - hidrógeno puro difieren ligeramente de las de la forma normal (orto). La distinción entre formas orto / para también se presenta en otras moléculas o grupos funcionales que contienen hidrógeno, tales como el agua o el metileno.

La interconversión no catalizada entre el para - hidrógeno y el orto - hidrógeno se incrementa al aumentar la temperatura; por esta razón, el H₂ condensado rápidamente contiene grandes cantidades de la forma orto que pasa a la forma paralentamente.¹⁴ La relación orto / para en el H₂ condensado es algo importante a tener en cuenta para la preparación y el almacenamiento del hidrógeno líquido: la conversión de la forma orto a la forma para es exotérmica y produce el calor suficiente para evaporar el hidrógeno líquido, provocando la pérdida del material licuado. Catalizadores para la interconversión orto / para, tales como compuestos de hierro, son usados en procesos de refrigeración con hidrógeno.

2D. RESONANCIA MAGNETICA NUCLEAR

Es un fenómeno físico basado en las propiedades mecánico-cuánticas de los núcleos atómicos. RMN también se refiere a la familia de métodos científicos que explotan este fenómeno para estudiar moléculas (espectroscopia de RMN), macromoléculas (RMN biomolecular), así como tejidos y organismos completos (imagen por resonancia magnética).
Todos los núcleos que poseen un número impar de protones o neutrones tienen un momento magnético y un momento angular intrínseco, en otras palabras, tienen un espín > 0. Los núcleos más comúnmente empleados en RMN son el protón (¹H, el isótopo más sensible en RMN después del inestable tritio, ³H), el ¹³C y el ¹⁵N, aunque los isótopos de núcleos de muchos otros elementos (²H, ¹⁰B, ¹¹B, ¹⁴N, ¹⁷O, ¹⁹F, ²³Na, ²⁹Si, ³¹P, ³⁵Cl, ¹¹³Cd, ¹⁹⁵Pt) son también utilizados.
Las frecuencias a las cuales resuena un núcleo atómico (i. e. dentro de una molécula) son directamente proporcionales a la fuerza del campo magnético ejercido, de acuerdo con la ecuación de la frecuencia de precesión de Larmor. La literatura científica hasta el 2008 incluye espectros en un gran intervalo de campos magnéticos, desde 100 nT hasta 20 T). Los campos magnéticos mayores son a menudo preferidos puesto que correlacionan con un incremento en la sensibilidad de la señal. Existen muchos otros métodos para incrementar la señal observada. El incremento del campo magnético también se traduce en una mayor resolución espectral, cuyos detalles son descritos por el desplazamiento químico y el efecto Zeeman.
La RMN estudia los núcleos atómicos al alinearlos a un campo magnético constante para posteriormente perturbar este alineamiento con el uso de un campo magnético alterno, de orientación ortogonal. La resultante de esta perturbación es el fenómeno que explotan las distintas técnicas de RMN. El fenómeno de la RMN también se utiliza en la RMN de campo bajo, la RMN de campo terrestre y algunos tipos de magnetómetros.

http://www.fullquimica.com/2010/10/particulas-subatomicas-fundamentales.html 

http://www.sc.ehu.es/sbweb/fisica/estadistica/sternGerlach/sternGerlach.html